Problem srednjeveškega matematika Leonarda Fibonaccija o zajcih

Poglejmo, kako raste število kuncev v prvih šestih mesecih:

1. mesec. En par mladih zajcev.

2. mesec. Še vedno obstaja en originalni par. Kunci še niso dosegli rodne starosti.

3. mesec. Dva para: prvotni, ki je dosegel rodnost + par mladih kuncev, ki jih je rodila.

4. mesec. Trije pari: en prvotni par + en par kuncev, ki jih je skotila v začetku meseca + en par kuncev, ki so se skotili v tretjem mesecu, vendar še niso dosegli spolne zrelosti.

5. mesec. Pet parov: en izvirni par + en par, rojen v tretjem mesecu in dopolnjen v rodni dobi + dva nova pari, ki so jim rodili + en par, ki se je rodil v četrtem mesecu, vendar še ni dosegel Zrelost.

6. mesec. Osem parov: pet parov iz prejšnjega meseca + trije novorojeni pari. Itd.

Da bo bolj jasno, prejete podatke zapišemo v tabelo:

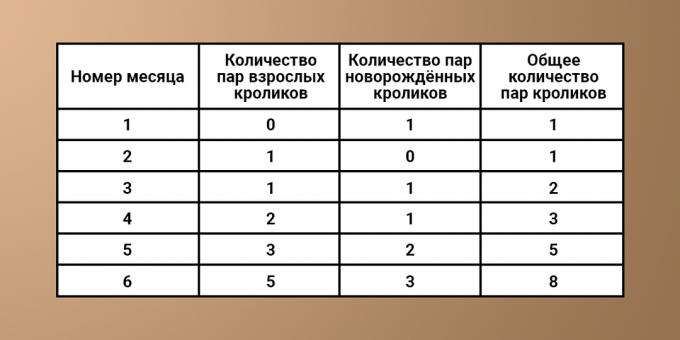
Če natančno preučite tabelo, lahko prepoznate naslednji vzorec. Vsakokrat je število kuncev, prisotnih v n. Mesecu, enako številu kuncev v (n - 1). Prejšnjem mesecu, povzeto s številom novorojenih kuncev. Njihovo število pa je enako skupnemu številu živali v mesecu (n - 2) (to je bilo pred dvema mesecema). Od tu lahko sklepate

formula:

F_n = F_{n - 1}+ F_{n - 2},

kjer je F_n - skupno število parov kuncev v n -tem mesecu, F_{n - 1} Ali je skupno število parov zajcev v prejšnjem mesecu in F_{n - 2} - skupno število parov kuncev pred dvema mesecema.

Preštejmo število živali v naslednjih mesecih, ki ga uporabljajo:

7. mesec. 8 + 5 = 13.

8. mesec. 13 + 8 = 21.

9. mesec. 21 + 13 = 34.

10. mesec. 34 +21 = 55.

11. mesec. 55 + 34 = 89.

12. mesec. 89 + 55 = 144.

Mesec 13 (začetek naslednjega leta). 144 + 89 = 233.

Na začetku 13. meseca, torej na koncu leta, bomo imeli 233 parov zajcev. Od tega bo 144 parov odraslih, 89 pa mladih. Nastalo zaporedje 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 imenovane Fibonaccijeve številke. V njem je vsako novo končno število enako vsota prejšnja dva.